문학으로 수학을 깨달은 잊지 못할 경험
‘마주 보는 각의 크기가 같다’는 것을 양주동 박사의 수필 <몇 어찌>를 보고 이해한 적이 있었다. 수학책에 나오는 ‘기하’라는 말이 음차 된 것을 모르고, 한자의 의미 그대로 몇 기(畿), 얼마 하(何)로 해석하고는 도대체 ‘몇 어찌’가 무슨 말인지 궁금해 했던 일화를 담은 수필이다. 양 박사는 그날 기하수업에서 배웠던 ‘맞꼭지각의 크기는 같다’는 원리를 선생님과의 대화체로 풀어내고 있었다. 문학으로 수학을 깨달은 잊지 못할 경험이었다.

복식학급이라는 특수한 환경 속에서 담임교사로 지내면서 주베르(J. Joubert)가 남겼던 ‘가르치는 것은 두 번 배우는 것’이라는 말은 큰 도움이 됐다. 서로 알고 있는 것을 나누며, 함께 자랄 수 있다는 신뢰는 인문학에서 출발하여 TAI 협력학습 기반 ‘THINK 모형’으로까지 이어졌다. 미래의 교실이 무학년제로 운영될 것이라는 전망이 쏟아져 나오고 있지만, 아직 우리의 교육환경에서 학년의 구분은 매우 유의미하게 작동하고 있는 기제였기에 두 개의 학년으로 하나의 수업을 한다는 것은 결코 쉬운 도전이 아니었다.

그럼에도 불구하고 3·4학년 여덟 명 학생들은 인문학으로 소통하는 수학수업을 즐거워하고, 수학 시간을 기다리는 학생들로 성장했다. 문학·역사·철학은 수학수업에 적용되었을 때 매우 유의미한 교육적 효과를 가져다주었다. 비록 부족함이 많은 연구였지만, 지속적인 노력을 통해 더 나은 수업이 이루어질 수 있을 것으로 기대하며 지난 호 문학(文) 활용 수업사례에 이어 이번 호에서는 역사(史)를 활용한 수업사례, 다음 호에서는 철학(哲)을 활용한 수업사례를 소개한다.

역사(史)로 수학적 추론과 의사소통을 나누다
▶ 왜 역사인가?
역사는 과거에 일어났던 사건이나 인물에 대한 기록이다. 역사 속에서 학생들은 다양한 수학적 문제상황을 만날 수 있다. 그리고 추체험(追體驗)을 통해 고민하는 과정에서 스스로 다양한 의사소통을 하며, 문제해결방향을 찾으려 노력하게 된다. 인간의 다양한 생활 경험에 근거한 역사를 통해 학생들은 활동의 주인공이 될 수 있고, 새로운 방법으로 문제를 해결해 나가는 기회를 얻게 되며, 교실 속에서 활발한 추론과 의사소통이 이루어지게 된다.

▶ 역사는 어떻게 수학과 소통할 수 있을까?

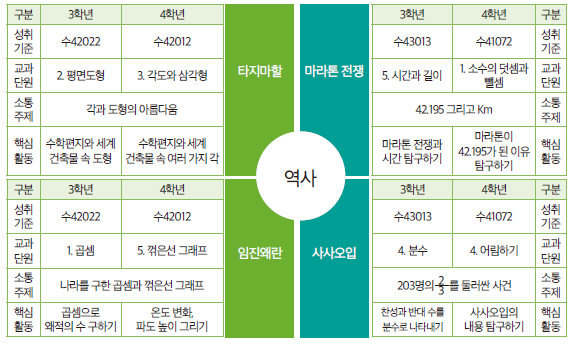
▶ 역사와의 소통으로 무엇을 얻을 수 있을까?

▶ 어떻게 활동했나요?
수업사례❶ _ <무굴제국과 타지마할>로 배우는 평면도형(3학년)과 각도(4학년)
오늘날까지도 세계에서 가장 아름다운 건축물로 꼽히며 인도의 대표적인 상징으로 자리 잡은 타지마할은 무굴제국의 역사를 간직하고 있다. 학생들은 아름다운 건축물을 통해 수학이 주는 아름다움을 경험할 수 있을 것이며, 타지마할의 벽면을 규칙적으로 완성해 나가거나 건축물에서 각과 도형을 찾는 활동을 통해, 수학적 개념과 용어를 사용하여 서로 소통하는 경험을 가질 수 있을 것이다.
[자세한 내용은 월간 새교육에 있습니다]